Procedural vs Conceptual Knowledge in
Mathematics Education
A Classroom Perspective
Before we start ...
|
This article is designed to cause the reader to reflect and to offer some ideas in regard to teaching mathematics in a way that prioritizes understanding in students. Despite containing one or two references to research, in no way is it intended to be an academic piece.
Terminology
In all articles and courses under the Learn Implement Share banner, I use the following terms interchangeably:
Interestingly, in my early years conducting professional development for teachers, I relied only on the terms ‘conceptual’ |
and ‘conceptual-based’ when presenting an effective conceptual approach to teaching mathematics. Until that is, I realized many course participants assumed I was promoting the idea that procedures were unimportant!!
I realized people saw the conceptual vs procedural argument as dualistic; that one had to be striving for either procedural knowledge OR conceptual knowledge.
Yet any approach to teaching mathematics should never be ONLY one or the other; it should always be a hybrid.
Similarly, I now use the following terms interchangeably:
I realized people saw the conceptual vs procedural argument as dualistic; that one had to be striving for either procedural knowledge OR conceptual knowledge.
Yet any approach to teaching mathematics should never be ONLY one or the other; it should always be a hybrid.
Similarly, I now use the following terms interchangeably:
- A procedural approach
- A Procedures-first, Understanding-second approach
- An approach that strives for procedural fluency/knowledge
- A Procedures-first approach
A Procedural Approach To Teaching Mathematics
In the article Why Students Need To Understand What They Are Working On For The Majority Of Lesson Time, I suggest that the procedural approach, still commonly used today, is as much a mindset as it is a strategy.
To illustrate this point, allow me to paint a picture of my early years as a teacher: When I walked into my maths classroom, my #1 priority was to teach the next few procedures of the unit and to have students gain sufficient practice of each procedure.
My aim was to have students develop procedural fluency. Although I knew I wasn’t directly addressing conceptual understanding in my students (because I didn’t know how to), I hoped (and assumed) that students would develop an understanding through their repeated practice of the procedures.
To illustrate this point, allow me to paint a picture of my early years as a teacher: When I walked into my maths classroom, my #1 priority was to teach the next few procedures of the unit and to have students gain sufficient practice of each procedure.
My aim was to have students develop procedural fluency. Although I knew I wasn’t directly addressing conceptual understanding in my students (because I didn’t know how to), I hoped (and assumed) that students would develop an understanding through their repeated practice of the procedures.
The ‘Procedures-first, Understanding-second’ Mindset
A good name for the scenario described above is a Procedures-first, Understanding-second mindset. This is because having a Procedures-first mindset reflects the fact that the number one focus and priority is to have students gain procedural fluency.
This was me! That students would understand what they were learning was my secondary intention. I hoped students would gain understanding once they had sufficiently practiced the procedures. By the way, I had more than a sneaky suspicion that a much better way of presenting mathematics existed, but I also knew I had absolutely no idea what that was. I wanted to focus on the next generation of aha moments in students, but I simply didn't know how. I was doing my best with the knowledge I had at the time.
This was me! That students would understand what they were learning was my secondary intention. I hoped students would gain understanding once they had sufficiently practiced the procedures. By the way, I had more than a sneaky suspicion that a much better way of presenting mathematics existed, but I also knew I had absolutely no idea what that was. I wanted to focus on the next generation of aha moments in students, but I simply didn't know how. I was doing my best with the knowledge I had at the time.
What the Procedures-first, Understanding-second approach looked like in my classroom
A procedural approach aims to make students proficient with procedures. I think we all have a pretty good idea of what a procedural approach looks like in the classroom. My efforts to have students gain procedural fluency were not much different from the norm. I’d begin with a procedure after, perhaps, some sort of (hopefully) engaging introduction.
Students would copy down the procedure and follow with 5-10 examples of the same type. The next procedure would follow, and then the next block of questions based on that procedure. Sure, I would weave in the occasional game, or competition, or applied activity - something to break the routine - but the default pedagogy was to teach procedures and have students successfully work through blocks of questions specific to each procedure.
Of course, towards the end of the unit would come the mixed questions followed by ‘the test’, now referred to as ‘the assessment task’. One of the key components to attaining procedural fluency in my students was Block Practice. I never knew it was called Block Practice back then, due to the lack of apparent alternative probably because I hadn’t realized there was an alternative (and without an alternative, there is little need to make the default practice). Block practice was simply THE way students practice mathematics.
Students would copy down the procedure and follow with 5-10 examples of the same type. The next procedure would follow, and then the next block of questions based on that procedure. Sure, I would weave in the occasional game, or competition, or applied activity - something to break the routine - but the default pedagogy was to teach procedures and have students successfully work through blocks of questions specific to each procedure.
Of course, towards the end of the unit would come the mixed questions followed by ‘the test’, now referred to as ‘the assessment task’. One of the key components to attaining procedural fluency in my students was Block Practice. I never knew it was called Block Practice back then, due to the lack of apparent alternative probably because I hadn’t realized there was an alternative (and without an alternative, there is little need to make the default practice). Block practice was simply THE way students practice mathematics.
What is Block practice?
Block Practice is the use of question banks that have students working from one question to the next without needing to apply cognitive thought beyond that required to follow a pre-taught procedure. Here’s one example of Block Practice from this article.
b) 4, 7, 9, 2, 2, 4
c) 2, 5, 3
d) 8, 4, 6, 2, 0, 3, 0
The outcomes of Block Practice are summarized in the following graphic:
- Find the mean of the following sets of scores:
b) 4, 7, 9, 2, 2, 4
c) 2, 5, 3
d) 8, 4, 6, 2, 0, 3, 0
The outcomes of Block Practice are summarized in the following graphic:
It appears that Block Practice is a key component to all-or-nearly-all procedural approaches to teaching mathematics, and it has been gaining attention in recent years.
Given we are addressing a practice that aims to impart procedural knowledge in students, it is interesting to note that the outcomes of Block Practice are similar to the following definition of procedural knowledge:
Given we are addressing a practice that aims to impart procedural knowledge in students, it is interesting to note that the outcomes of Block Practice are similar to the following definition of procedural knowledge:
(Procedural Knowledge is) learning that involves only memorizing operations with no understanding of underlying meanings.’ Arslan (2010)
|
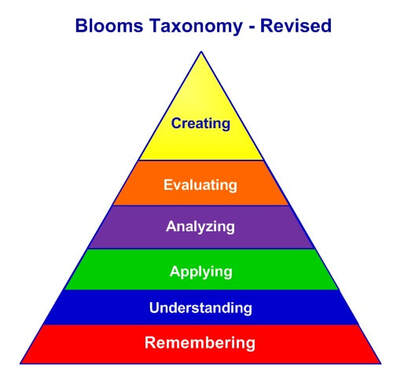
And memorizing operations with no understanding of underlying meanings requires very little cognitive effort - it sits at the lowest rung on Bloom’s Taxonomy’ (See image at left) Blocked Practice was most definitely the fashion in my early years of teaching (The eighties, last century), but it turns out that it is still the rage today! One recent analysis of six popular (US) middle school math textbooks found that, on average, more than 80% of the practice problems were blocked. ( Rohrer, Dedrick, Agarwal, © 2017, p7) |
Transitioning to an Understanding-first approach to teaching mathematics
My transition certainly didn’t happen overnight. It took a lot of thinking and many trials of ideas over numerous years. My transition was aided by the fact that my career path was rather different from the norm - I had a fifteen-year stretch which included multiple-year periods where my primary work was math tuition and casual teaching.
This meant that I had headspace, a luxury most teachers do not have! Added to this, I had the fortune of periods of permanent teaching in schools with tiny math departments. Very tiny math departments, in fact - of the type where, essentially, I WAS the department. And when the department grew, I was given the lead. So I had no one standing in my way when it came to implementing new pedagogies.
Although I had grasped the importance of student-centred learning and of creating a need to learn in students, the transition resulted from me pretty-much following my own nose. I wasn’t directly chasing higher student scores. Rather, I was finding ways to work with students to co-create a learning environment that:
I wouldn’t say I discovered any new educational principles. Instead, I discovered principles that I later found out had already been discovered. One such principle was interleaving, which we’ll address shortly.
This meant that I had headspace, a luxury most teachers do not have! Added to this, I had the fortune of periods of permanent teaching in schools with tiny math departments. Very tiny math departments, in fact - of the type where, essentially, I WAS the department. And when the department grew, I was given the lead. So I had no one standing in my way when it came to implementing new pedagogies.
Although I had grasped the importance of student-centred learning and of creating a need to learn in students, the transition resulted from me pretty-much following my own nose. I wasn’t directly chasing higher student scores. Rather, I was finding ways to work with students to co-create a learning environment that:
- was collaborative
- had students intrinsically fired-up to explore math
- enabled me to bring students onto my page
- created a palpable buzz of learning, and
- maximized the occurrence of aha moments.
I wouldn’t say I discovered any new educational principles. Instead, I discovered principles that I later found out had already been discovered. One such principle was interleaving, which we’ll address shortly.
The Understanding-first, Procedures-second approach - What it looks like in the classroom.
An Understanding-first, (Procedures-second) approach can be many things - the breadth of possibilities is much wider than for a Procedures-first, (Understanding-second) approach. Very simply, it is an approach that places an obvious focus on having students understand new work from the get-go. Where possible, it has students working with the concepts underpinning a procedure before they are taught that procedure. Ideally, and where appropriate, students are given a chance to discover the procedure for themselves.
|
Conversely, an Understanding-first, Procedures-second approach avoids at all costs teaching students a procedure when they don’t understand the underlying concepts. Importantly, a teacher using an Understanding-first approach will know that ‘teaching-by-telling’ is an ineffective way to impart concepts to students.
In other words, the teacher will realize that the traditional theory-based lecture format is an inefficient way to impart understanding because concepts are almost always gained through tangential means; rarely directly. |
For example, concepts are imparted through higher-order questioning, use of analogies, the presentation of conceptually-based diagrams and illustrations, the use of animations, and through making connections with prior knowledge.
Granted, some math units are more difficult to present conceptually than others, but where possible, the above principles are employed. Although some Block Practice will inevitably be used in an Understanding-first approach, the use of Block Practice is best kept to a minimum, and where appropriate, replaced with a different form of practice - interleaving.
Granted, some math units are more difficult to present conceptually than others, but where possible, the above principles are employed. Although some Block Practice will inevitably be used in an Understanding-first approach, the use of Block Practice is best kept to a minimum, and where appropriate, replaced with a different form of practice - interleaving.
Interleaving Explained
To quote from this article, the aim of interleaving is to intentionally have students working on several related ideas simultaneously so that the opportunity to ‘blindly follow’ a procedure is removed. Setting tasks that require students to engage with several connected concepts results in students reasoning, thinking cognitively and choosing appropriate procedures.
|
Interleaving is inherently more engaging for students because it creates in them an innate sense that they are tangibly involved in the process; thinking things through. Interleaving pushes the practice higher up Bloom’s Taxonomy triangle.
The free Conceptual Trigonometry Tutorial is a clear demonstration of the Understanding-first, Procedures-second approach. Rather than presenting right-angled trig traditionally and using block practice to have students practice the procedures, this approach has students working through - from the very first lesson - an interleaved set of questions. |
The approach requires students to first determine the type of trig question they are faced with and then apply the appropriate procedure to solve. Students are able to do this because during the first half of the lesson, they gained a strong conceptual understanding through the use of conceptually-based GeoGebra and Powerpoint files as well as a pedagogy that demystifies trigonometry.
On the surface, this approach to right-angled trig appears more difficult than the traditional. It LOOKS more difficult, but to students, it isn’t. Students find this conceptual approach easier because they understand what it is they are doing. They are not ‘mindlessly’ following procedures that make no sense to them. Rather, the approach empowers students as they apply their new understanding to make decisions and calculate their answers.
Why is this approach significantly more engaging for students than the Procedures-first alternative? Very simply because students get their hands dirty - thinking, reasoning, making decisions, drawing on their understanding.
On the surface, this approach to right-angled trig appears more difficult than the traditional. It LOOKS more difficult, but to students, it isn’t. Students find this conceptual approach easier because they understand what it is they are doing. They are not ‘mindlessly’ following procedures that make no sense to them. Rather, the approach empowers students as they apply their new understanding to make decisions and calculate their answers.
Why is this approach significantly more engaging for students than the Procedures-first alternative? Very simply because students get their hands dirty - thinking, reasoning, making decisions, drawing on their understanding.
But (I hear you say) I already do this !?!
It may be that you already employ a similar approach to teaching mathematics. But the question is - do you realize the power of the approach you use? Are you aware of WHY the approach is highly effective? I often have course participants work through tutorials and say ‘Wow - I do that, but I never realized it was a thing! I’m going to hone this skill now. Thanks!’ So I recommend you work through the free tutorial to help make you more aware of your current teaching methods, so that you are better-able to capitalize on these methods into the future.
Conceptual Coordinate Geometry (Straight line graphing)
Another obvious unit to employ the Understanding-first, procedures-second approach, is Coordinate Geometry (Straight line graphing). This is a topic that is so important for students to conceptually understand before they face pre-calculus.
In fact, for my first attempt - in 2010 - at comprehensively demonstrating this conceptual approach to teachers, I chose the Coordinate Geometry topic. After many upgrades, that attempt has now become the course that I refer to as Conceptual Coordinate Geometry.
The approach is hugely fun to teach. It has students, within the second lesson, being able to view a simple straight-line graph (e.g. y = ⅔ x + 4) and directly read its equation - AND conversely, upon being presented with a simple linear equation, be able to directly sketch its graph. No algebra. No messy tables of values! No ‘I hate this - I want out!’
The way the unit is assembled and the fact that it is mostly student-centered allows for differentiated instruction and peer learning, aspects that help make the approach engaging.
In addition to the pedagogies presented, this approach features an extensive, conceptually-based worksheet document which has students working with the concepts from the get-go. Importantly, the approach fosters student agency.
In fact, for my first attempt - in 2010 - at comprehensively demonstrating this conceptual approach to teachers, I chose the Coordinate Geometry topic. After many upgrades, that attempt has now become the course that I refer to as Conceptual Coordinate Geometry.
The approach is hugely fun to teach. It has students, within the second lesson, being able to view a simple straight-line graph (e.g. y = ⅔ x + 4) and directly read its equation - AND conversely, upon being presented with a simple linear equation, be able to directly sketch its graph. No algebra. No messy tables of values! No ‘I hate this - I want out!’
The way the unit is assembled and the fact that it is mostly student-centered allows for differentiated instruction and peer learning, aspects that help make the approach engaging.
In addition to the pedagogies presented, this approach features an extensive, conceptually-based worksheet document which has students working with the concepts from the get-go. Importantly, the approach fosters student agency.
We’ve only dipped our toes in …
Despite having merely scratched the surface, I hope this article has given you a classroom-based sense of the Understanding-first, Procedures-second approach.
I could, of course, expand this article to fifteen-plus hours worth of reading and video on how to effectively deliver such an approach. But that would be silly because we already have a 15-hour course that achieves this. If you are not yet ready for such a course, check out the blog for other articles and free tutorials.
GeoGebra - Arguably the easiest way to bring aha moments to students (within many math concepts). Although this isn’t a GeoGebra-specific article, no discussion of conceptual knowledge and conceptual approaches to teaching mathematics would be complete without mentioning GeoGebra. Although in this case, the mentioning of GeoGebra comes with a caveat - I refer to the PROFICIENT use of GeoGebra.
I could, of course, expand this article to fifteen-plus hours worth of reading and video on how to effectively deliver such an approach. But that would be silly because we already have a 15-hour course that achieves this. If you are not yet ready for such a course, check out the blog for other articles and free tutorials.
GeoGebra - Arguably the easiest way to bring aha moments to students (within many math concepts). Although this isn’t a GeoGebra-specific article, no discussion of conceptual knowledge and conceptual approaches to teaching mathematics would be complete without mentioning GeoGebra. Although in this case, the mentioning of GeoGebra comes with a caveat - I refer to the PROFICIENT use of GeoGebra.
By proficient, I mean using GeoGebra for a myriad of topics in addition to graphing and geometry (for example, rates, ratios, fractions, number, trigonometry, similarity, Venn diagrams, measurement and many scenarios based on formulas). And by ‘proficient’ I mean being able to create files that are an exact extension of the way you want to teach.
When teachers become proficient with GeoGebra - according to the above definition - they invariably experience a profound shift in their teaching.
Through their proficient use of GeoGebra they are able to significantly improve their students’ engagement and understanding of many types of math without needing to significantly alter their overall approach to teaching.
When teachers become proficient with GeoGebra - according to the above definition - they invariably experience a profound shift in their teaching.
Through their proficient use of GeoGebra they are able to significantly improve their students’ engagement and understanding of many types of math without needing to significantly alter their overall approach to teaching.
If you are interested in becoming more proficient with GeoGebra but aren’t prepared to purchase a $500 course, then the Taster is for you. The GeoGebra-Proficiency Taster is a quarter of the full $495 course for only $5.
Over to you ...
In this article, I have unpacked several reasons in favour of transitioning from a Procedures-first approach to one that prioritizes understanding first and procedures second. I have given a glimpse of what this approach looks like in the classroom. I’ve referenced other articles, free tutorials, as well as part and full courses as roadmaps for you to follow to help you embrace an Understanding-first approach. I know we have barely scratched the surface.
However, this is a massive topic, and this article is already over-sized for my standards. I’d love to know whether the ideas in this article are new to you and if they are, whether you are skeptical of the approach. Or perhaps the ideas expressed are in line with the way you teach. Either way, I’d love to hear your responses.
NOTE: Create a Hyvor account before commenting (click LOGIN) -that way you'll be notified of replies and you won't be anonymous.
If you don't create an account, please state your name at the start of your comment. Thanks.
However, this is a massive topic, and this article is already over-sized for my standards. I’d love to know whether the ideas in this article are new to you and if they are, whether you are skeptical of the approach. Or perhaps the ideas expressed are in line with the way you teach. Either way, I’d love to hear your responses.
NOTE: Create a Hyvor account before commenting (click LOGIN) -that way you'll be notified of replies and you won't be anonymous.
If you don't create an account, please state your name at the start of your comment. Thanks.