Exploring Pi With GeoGebra
The Case For All Middle & High School Mathematics Teachers To Become Proficient Users Of GeoGebra
Transform your math teaching with GeoGebra.
Conceptual understandingThe article Teaching Mathematics using an approach that is both conceptual and procedural sheds some light on the conceptual approach to teaching mathematics. In the article, I state that mathematical understanding is fostered through activities and strategies designed to engineer aha moments in students.GeoGebra is an incredibly powerful and easy-to-use tool that math teachers can use to help impart conceptual understanding to students. This article promotes the idea that (all) middle and high school mathematics teachers ought to be regularly utilising GeoGebra.
As I argue in Let GeoGebra transform your mathematics teaching, there appears to be an unnecessarily high portion of math teachers who do not regularly utilise GeoGebra to a deep level. The main reason for this, I believe, is a lack of awareness of the power of GeoGebra and its applicability to so many aspects of mathematics. Exploring pi with GeoGebra |
Check out the new LIS Course Academy Short-courses Mini-courses Micro-courses Previews of extensive courses |
Observe the GeoGebra file in the image, showcasing the relationship between pi and a circle. It features a circle, its circumference and diameter displayed dynamically.
And yes, this is deliberately a simple file. Yet when some dynamic text is added to calculate the quotient, we end up with … pi!
This simple file illustrates the power of GeoGebra in visually encapsulating the derivation of pi using circumference and diameter. It can be used as a summary after students have manually explored circles, a visual introduction to the topic, or as a starting point for student-led investigations.
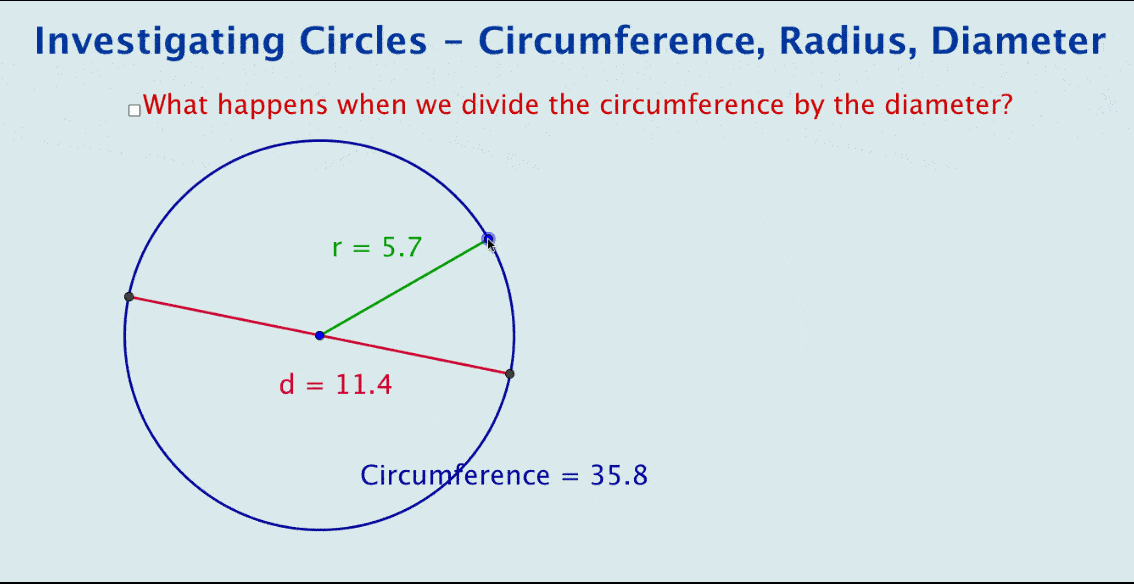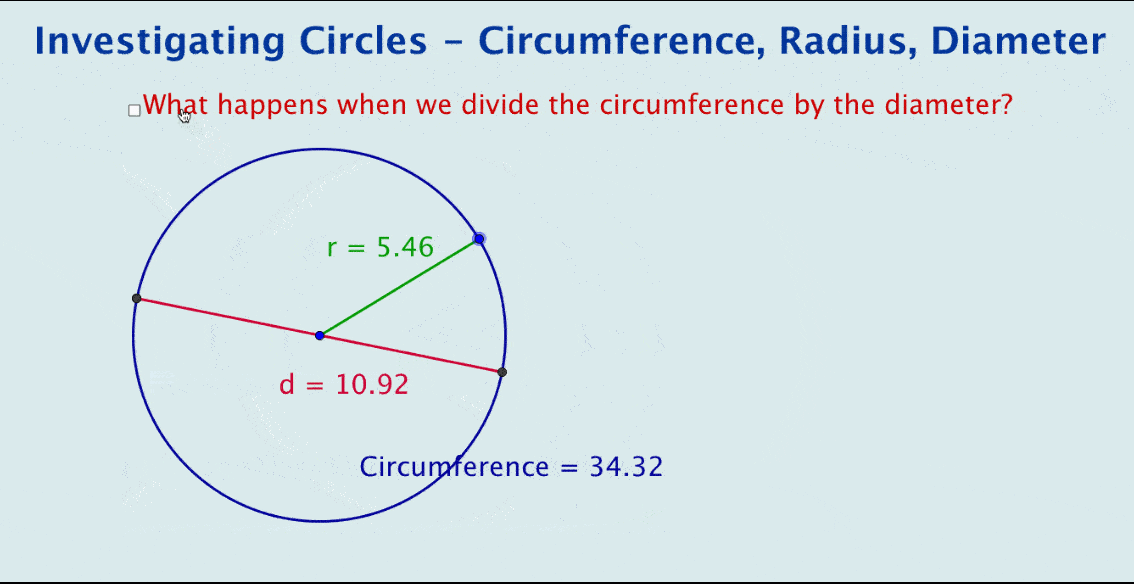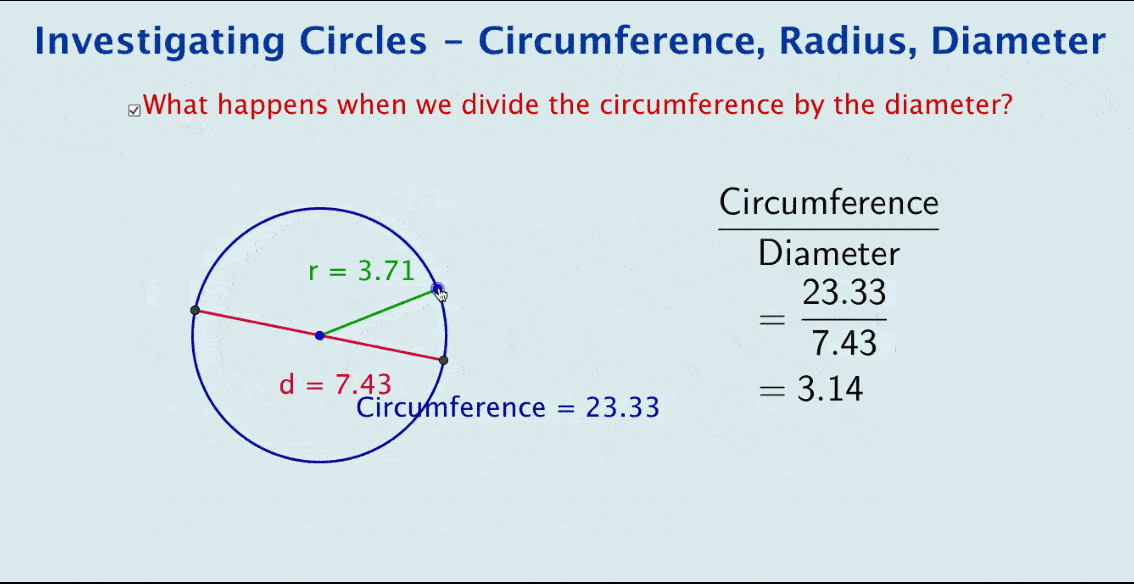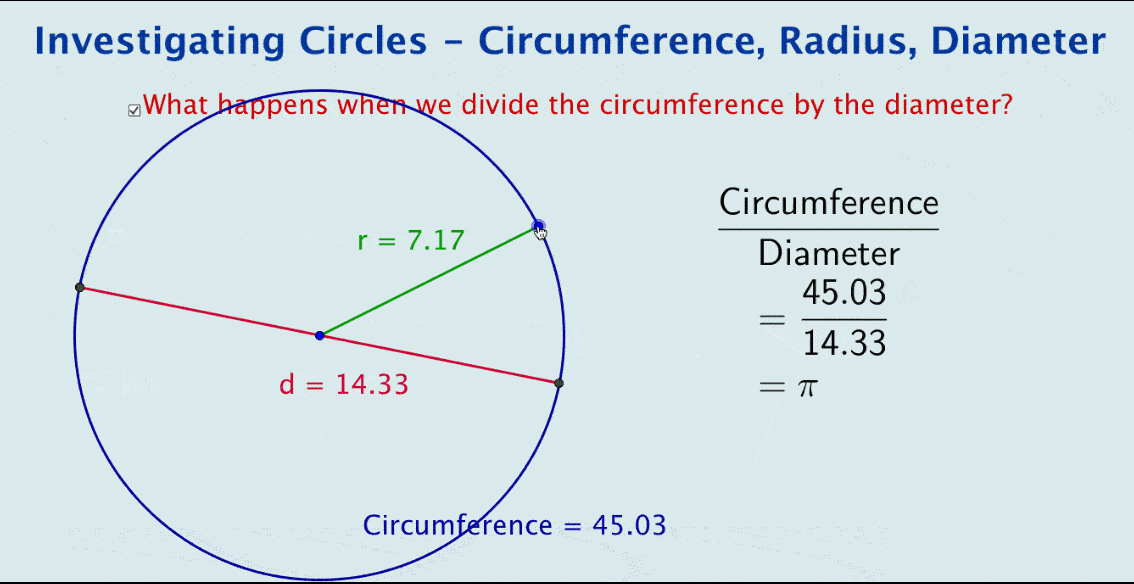
Now consider the dynamic image below.
And yes, this is deliberately a simple file. Yet when some dynamic text is added to calculate the quotient, we end up with … pi!
This simple file illustrates the power of GeoGebra in visually encapsulating the derivation of pi using circumference and diameter. It can be used as a summary after students have manually explored circles, a visual introduction to the topic, or as a starting point for student-led investigations.
Now consider the dynamic image below.
Use GeoGebra files for teacher-led investigations
Now that students have seen the relationship between diameter and circumference, the original GeoGebra file (not the gif) could be used as a teacher-led, guided investigation.
Using the dynamic quotients, students can explore mathematical systems by asking, "Can we find a relationship between area and one of the other quantities?" and using the dynamic quotients.
Note, you could include more explorations or create several files for this exploration. In addition, the file could be pre-made or if you are proficient, you could create the dynamic quotients as students suggest possible relationships.
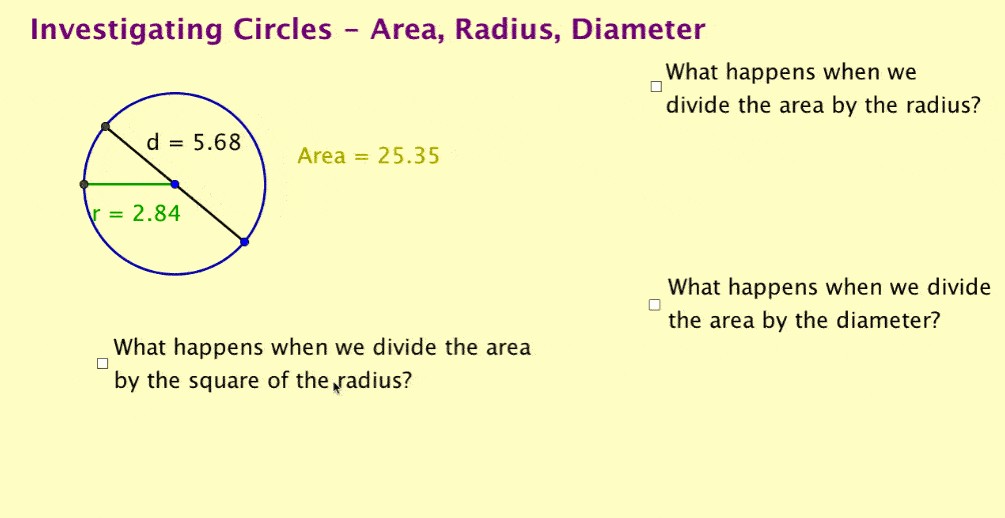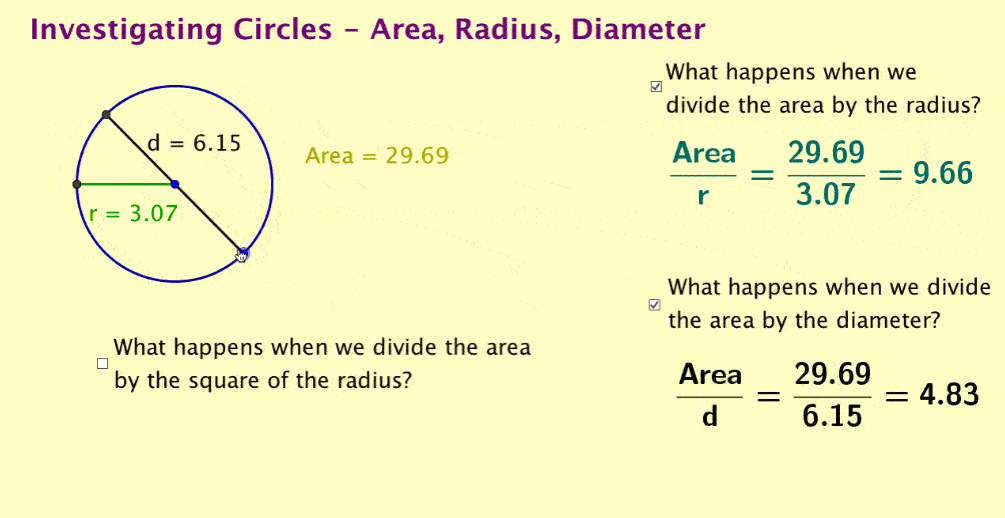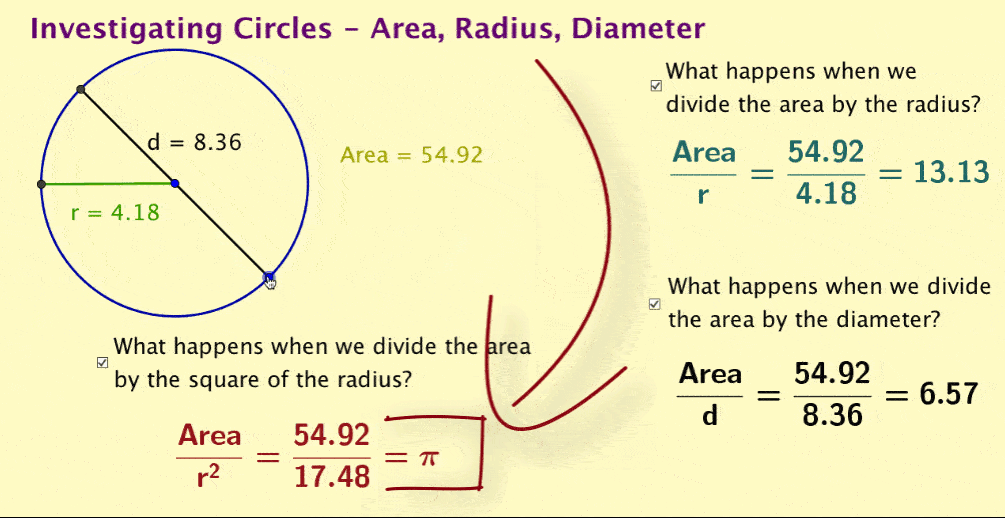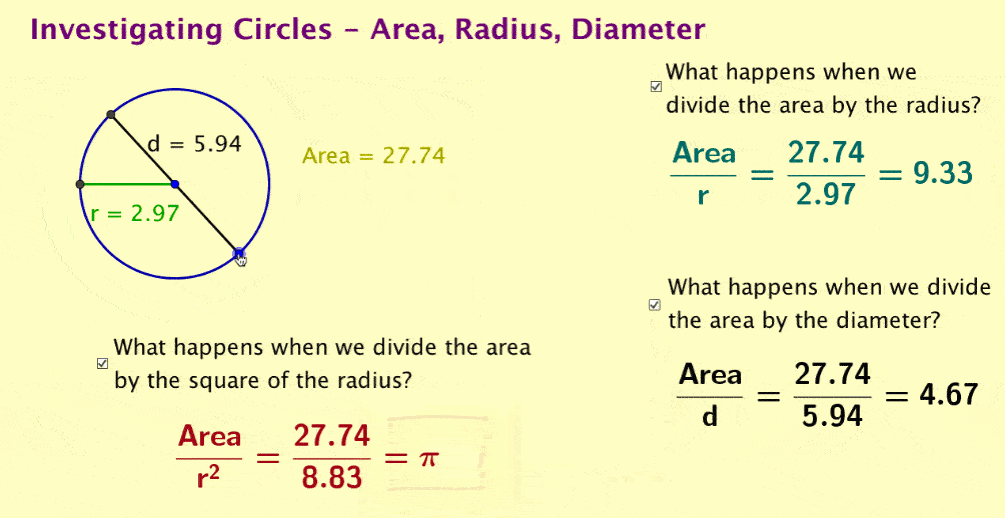
Note also that dividing area by the square of the radius will not be an intuitive relationship for students to suggest and may require considerable probing of students to have them suggest this. If students can create dynamic formulas, they could be set free on a search to discover pi within the area relationship.
All this is a great deal of fun – very engaging for students and very much about exploring mathematical systems. (And isn’t this what maths education is supposed to be about?) This activity is engaging and an excellent demonstration of the ease of using GeoGebra as an educational tool.
Find the ‘Surf Board’ GeoGebra file created by Anne Wolkowitsch halfway down the article, Are you utilising GeoGebra? The file promotes conceptual understanding and comes with a suggested approach for demonstration. The file is available for download.
Using the dynamic quotients, students can explore mathematical systems by asking, "Can we find a relationship between area and one of the other quantities?" and using the dynamic quotients.
Note, you could include more explorations or create several files for this exploration. In addition, the file could be pre-made or if you are proficient, you could create the dynamic quotients as students suggest possible relationships.
Note also that dividing area by the square of the radius will not be an intuitive relationship for students to suggest and may require considerable probing of students to have them suggest this. If students can create dynamic formulas, they could be set free on a search to discover pi within the area relationship.
All this is a great deal of fun – very engaging for students and very much about exploring mathematical systems. (And isn’t this what maths education is supposed to be about?) This activity is engaging and an excellent demonstration of the ease of using GeoGebra as an educational tool.
Find the ‘Surf Board’ GeoGebra file created by Anne Wolkowitsch halfway down the article, Are you utilising GeoGebra? The file promotes conceptual understanding and comes with a suggested approach for demonstration. The file is available for download.
Here’s what one teacher had to say about becoming more proficient with GeoGebra:
I found the course extremely helpful and relevant to my teaching. I was aiming to improve my knowledge of GeoGebra and to be able to create my own files. The course equipped me for this and I feel much more confident in using GeoGebra in my classes and have done so in a number of classes and topic areas. Sally De Maria, 26/05/201
What other topics come to mind that GeoGebra could be applied to (other than graphing and geometry)? Do you utilise GeoGebra widely? Are you tempted to use it more? We'd love your thoughts below!
NOTE: Create a Hyvor Talk account before commenting (click LOGIN) -that way you'll be notified of replies and you won't be anonymous.
If you don't create an account, please state your name at the start of your comment. Thanks.
NOTE: Create a Hyvor Talk account before commenting (click LOGIN) -that way you'll be notified of replies and you won't be anonymous.
If you don't create an account, please state your name at the start of your comment. Thanks.
