Developing Conceptual Understanding With GeoGebra
(The original GeoGebra file used for the dynamic image above was created by Pamela McGillivray, Broome Senior High School, WA, course participant, December 2012)
|
Teaching mathematics with a focus on conceptual understanding, combined with teaching procedures, is crucial.
There is a world of difference between students being able to ‘do mathematics’ and students understanding the mathematics they are 'doing'. As is evidenced by research, simply practising mathematical routines is not enough - developing conceptual understanding requires higher-level cognitive processes such as connecting ideas, reasoning, and solving complex problems (Silver et al., 2009; Stein & Lane, 1996) Therefore, a hybrid approach, where students explore concepts before learning the related procedures, is ideal. We refer to such an approach as an Understanding-first, Procedures-second Approach. The article Teaching Mathematics Using An Approach That Is Both Conceptual And Procedural sheds some light on a hybrid conceptual approach to teaching mathematics, one that also acknowledges the importance of teaching procedures. To quote J.E.Schwartz from his article: |
In a conceptually oriented mathematics class, the bulk of time is spent helping the students develop insight. Activities and tasks are presented to provide learners with experiences that provide opportunities for new understandings.
Introducing GeoGebra
GeoGebra is a powerful tool for enhancing mathematical understanding. GeoGebra allows students to gain a deeper understanding of mathematical concepts and principles, making practice more meaningful.
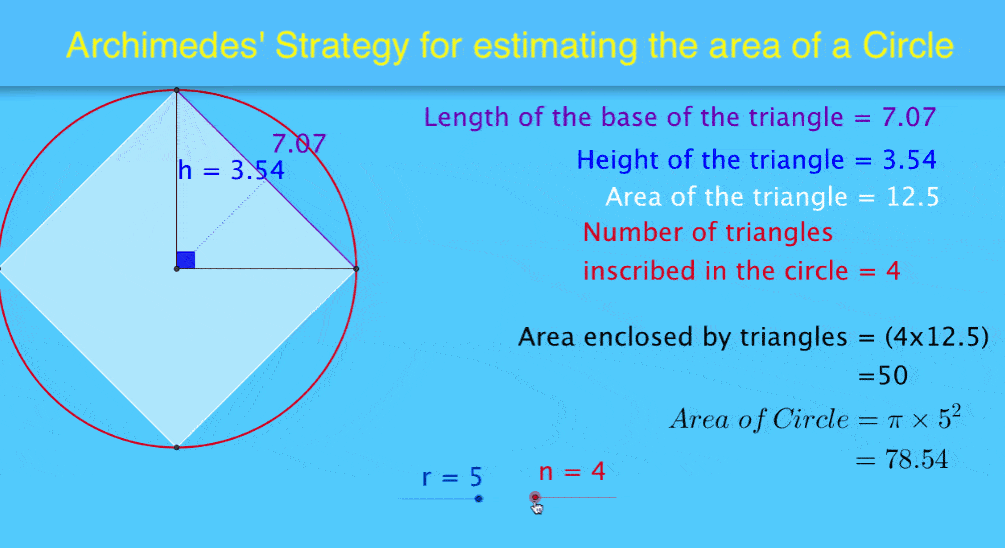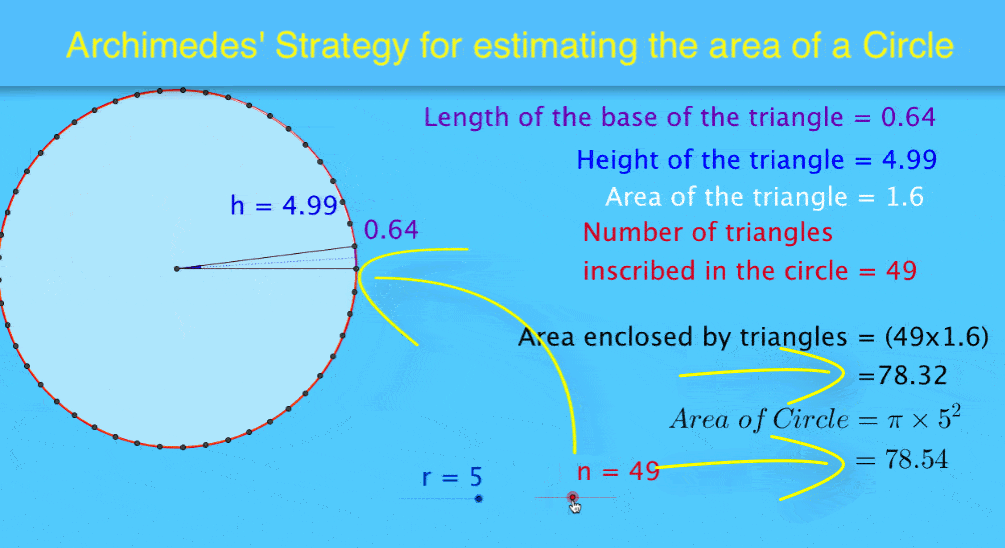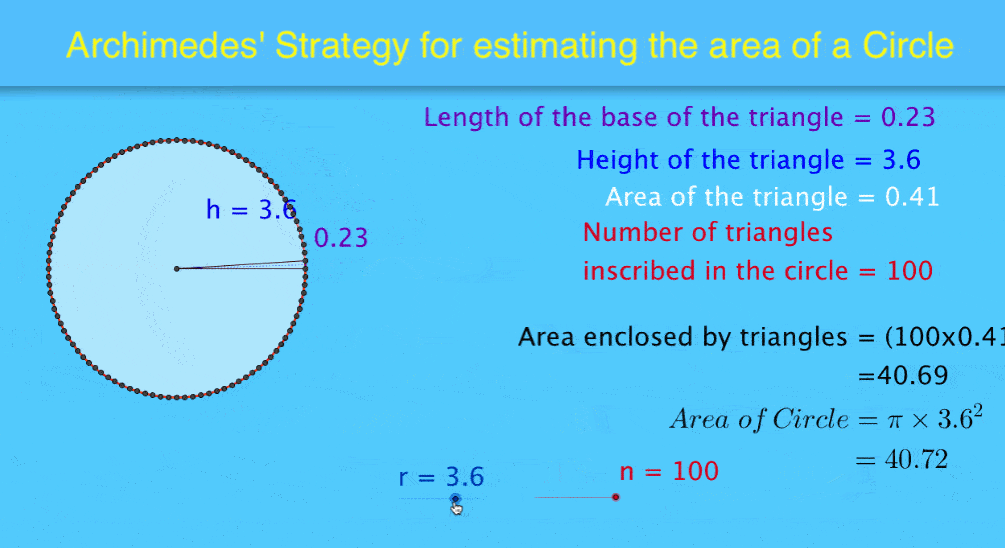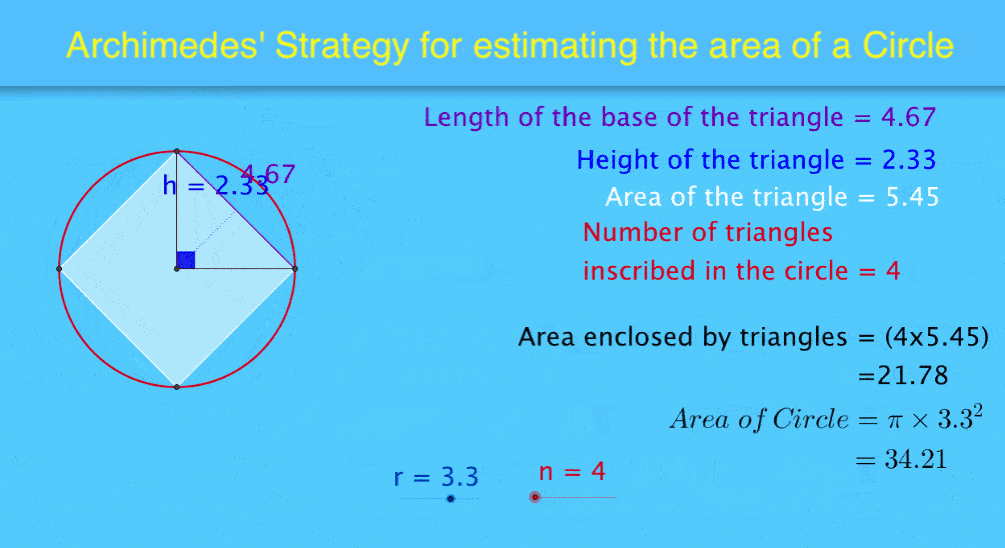
The dynamic image at the top of this article demonstrates this effectively. Observe how the two area sums change and approach the area of the circle as the variable 'n' increases.
The visual representation of the mathematical principle in this dynamic file leads to an increase in "aha" moments for students.
Of course, students still need to crunch the numbers underpinning the principle. However, to watch the two area sums change dynamically with changes in ‘n’ – and to witness the summed area triangles approach the area of the circle as ‘n’ increases – is stunningly powerful.
The dynamic image at the top of this article demonstrates this effectively. Observe how the two area sums change and approach the area of the circle as the variable 'n' increases.
The visual representation of the mathematical principle in this dynamic file leads to an increase in "aha" moments for students.
Of course, students still need to crunch the numbers underpinning the principle. However, to watch the two area sums change dynamically with changes in ‘n’ – and to witness the summed area triangles approach the area of the circle as ‘n’ increases – is stunningly powerful.
More aha moments without a change in pedagogy?
Files like the one above increase the occurrence of aha moments in students. However, demonstrating such a dynamic file, as powerful as it is, does not require a change in pedagogy. The only requirement is for the teacher to plug in a data projector, manipulate the file and ask leading questions.
There is an almost limitless number of mathematical situations to which GeoGebra can be applied – even when only used as a demonstration tool.
There is an almost limitless number of mathematical situations to which GeoGebra can be applied – even when only used as a demonstration tool.
One Teacher Had This To Say:
"I had (in the past) found Geogebra to be a not very intuitive piece of software, so learning some advanced applications was great. Using GeoGebra in class has greatly improved students' ability to visualise tricky concepts - like locus, linear and non-linear functions, trig relationships, etc. The online course was fantastic." Kathy Howard, Bathurst High Campus, 15.9.14 (2010 participant)
See GeoGebra in action - Some examples:
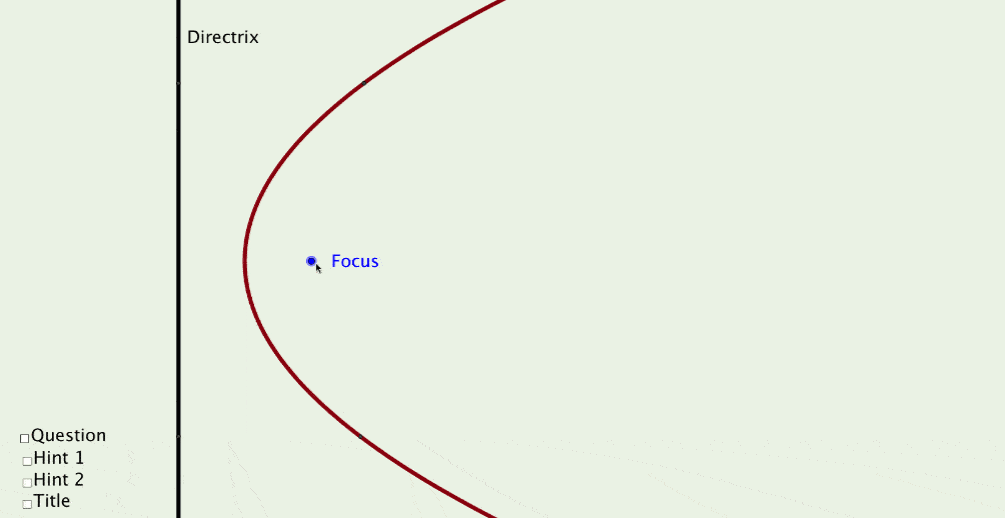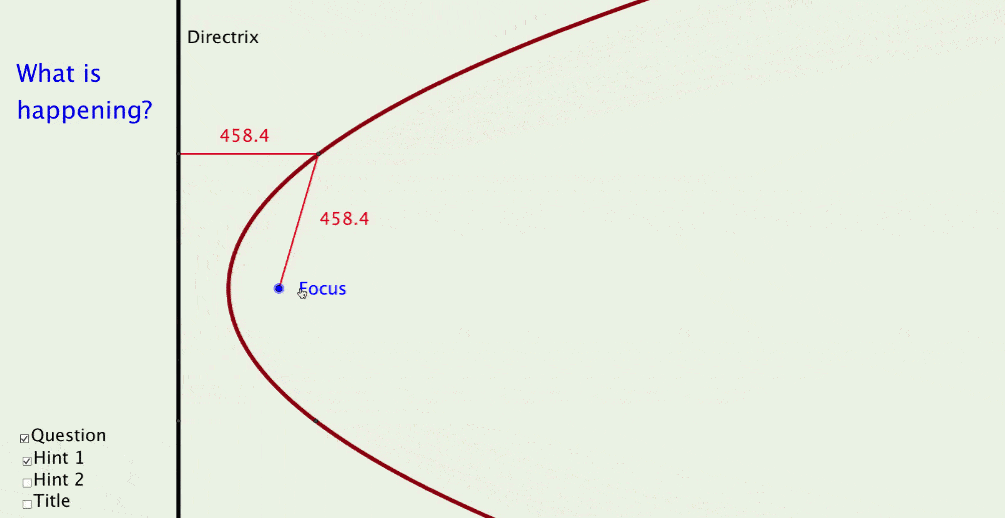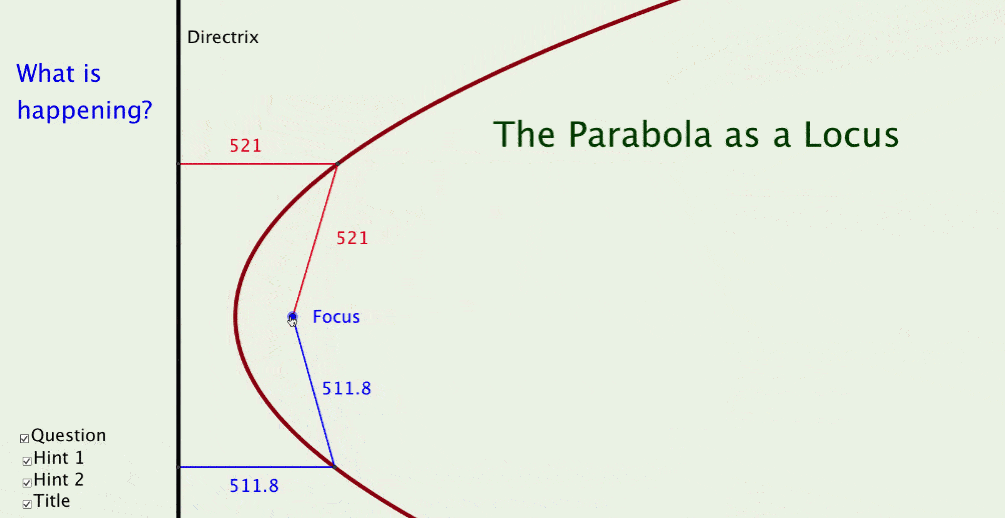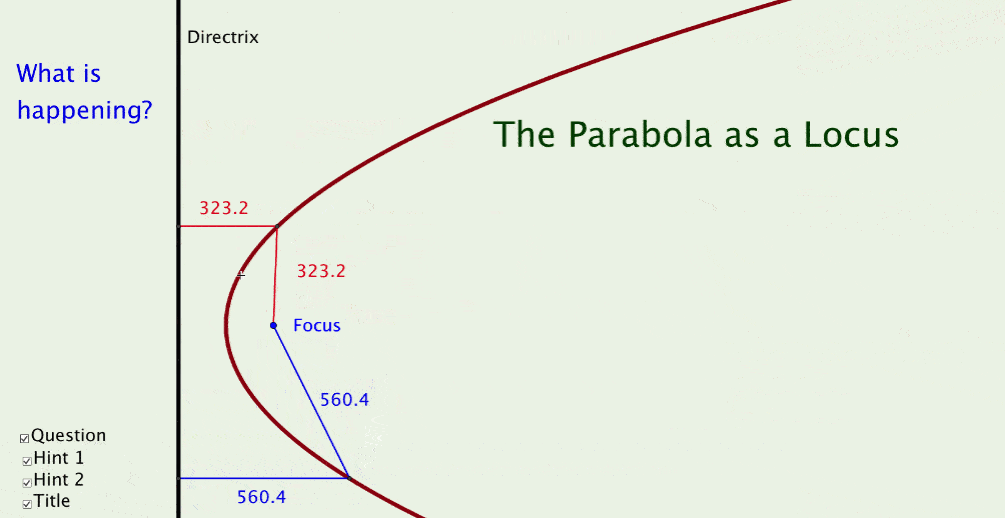
Parabola As A Locus File
Show students a well-designed GeoGebra file that visually demonstrates mathematical principles, such as the 'Parabola as a Locus' file. Encourage them to observe and ask questions.
(The original GeoGebra file used for the dynamic image above is one of the 50+ files which participants create)
Using A File As A Demonstration Experience
Use Files for Demonstrations - Project GeoGebra files before teaching maths concepts to spark interest and encourage inquiry. Pose leading questions and have students discuss them in pairs before sharing them with the class.
Advantages of using GeoGebra before teaching the associated mathematics
Using GeoGebra to foster inquiry before teaching the associated mathematics has benefits. These include increased student engagement, more aha moments, and higher-order thinking. All lead to deeper understanding.
GeoGebra also allows for mathematical investigations, as seen in the Pythagoras article. Even without disrupting the traditional teaching approach, GeoGebra can be used as a demonstration tool with just a projector and file.
GeoGebra also allows for mathematical investigations, as seen in the Pythagoras article. Even without disrupting the traditional teaching approach, GeoGebra can be used as a demonstration tool with just a projector and file.
The Surfboard File
Another excellent demonstration of a file designed to foster conceptual understanding is the Surfboard file, originally created by December 2013 participant Anne Wolkowitsch. You will find it halfway down this article, along with a suggested conceptually-based approach for demonstrating it. And you can also download the GeoGebra file from that page!
Do you use GeoGebra extensively? Can you modify files during teaching? Or do you only demonstrate files created by others?
Share your thoughts in the comments.
NOTE: Create a Hyvor account before commenting (click LOGIN) -that way you'll be notified of replies and you won't be anonymous.
If you don't create an account, please state your name at the start of your comment. Thanks.
Share your thoughts in the comments.
NOTE: Create a Hyvor account before commenting (click LOGIN) -that way you'll be notified of replies and you won't be anonymous.
If you don't create an account, please state your name at the start of your comment. Thanks.