A Pythagoras Investigation Using GeoGebra
How GeoGebra Opens Doors To New Discoveries
A Pythagoras investigation using GeoGebra
One day, I was playing around with GeoGebra and wanted to create a file that visually demonstrated Pythagoras' Theorem’s workings. I had junior high school students in mind. I wanted the file to cause students to respond with, “Aha, now I see that the sum of the two smaller areas is equal to the larger area is true." I was not consciously aware of the fact that I was undertaking a Pythagoras investigation!
The first file I created was the file dynamically represented below.
The first file I created was the file dynamically represented below.
And then I began to ponder ...
I was happy with the file. However, my Pythagoras investigation sparked some new thoughts not long after creating the file.
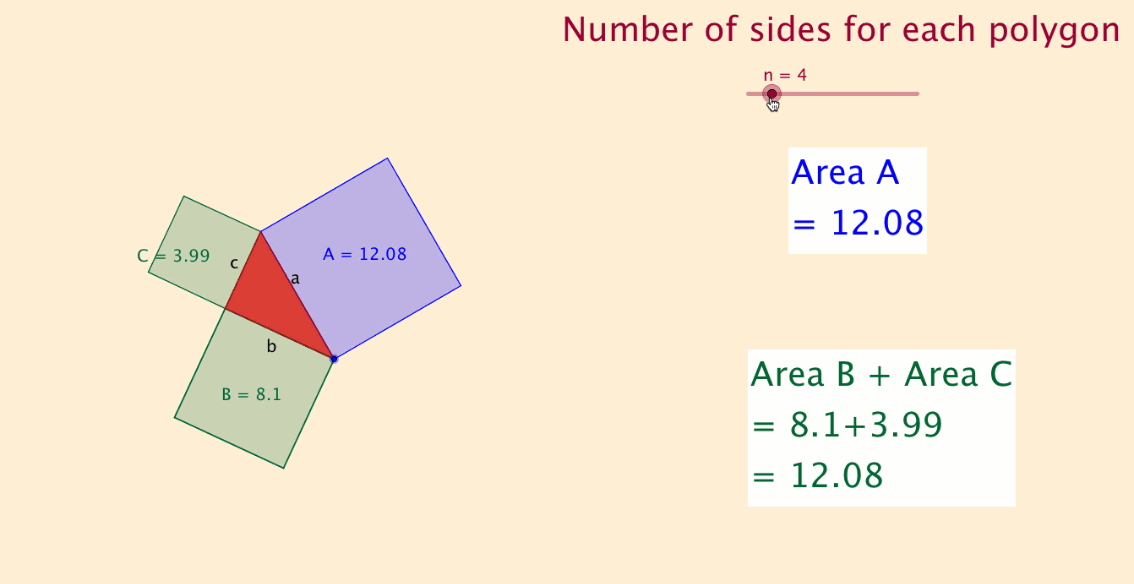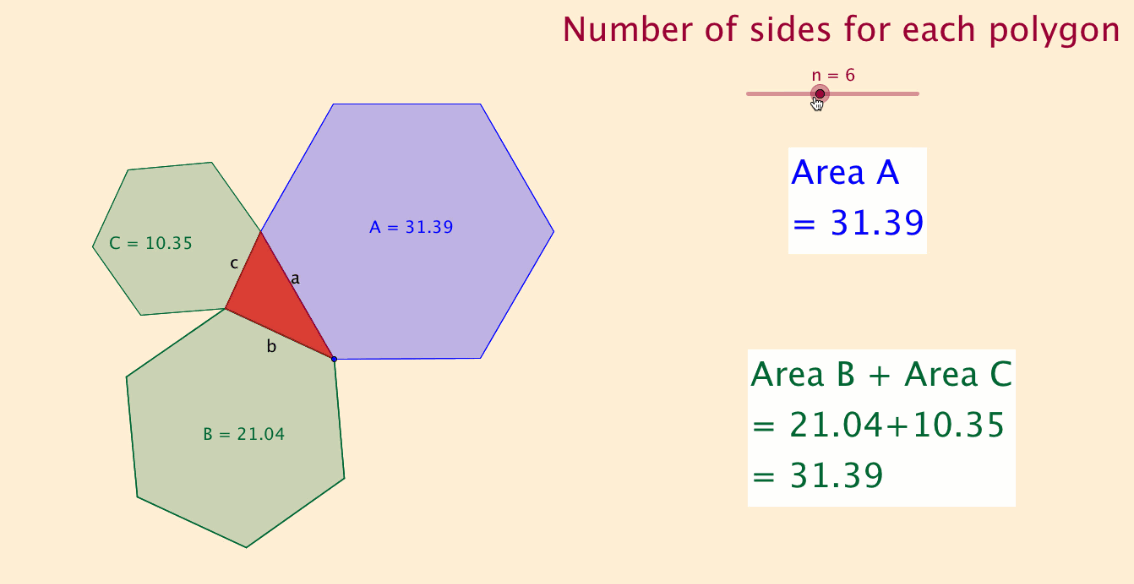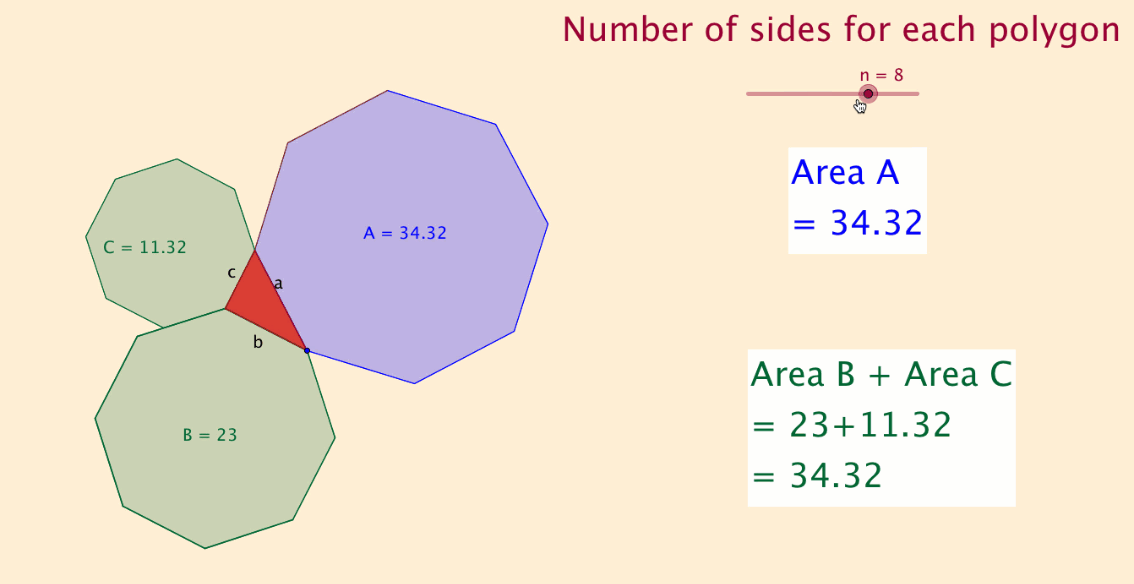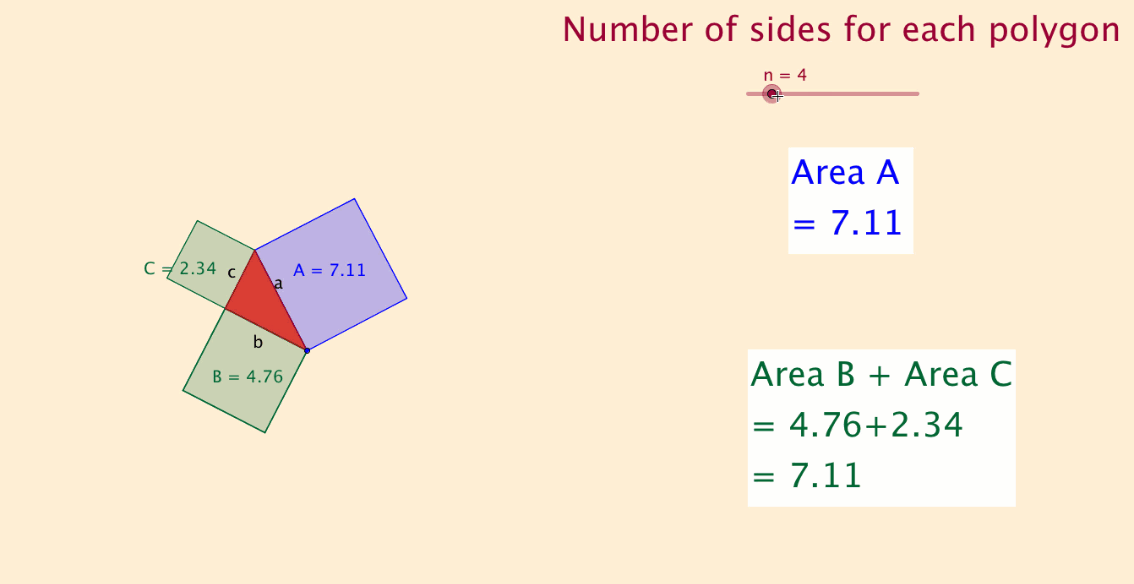
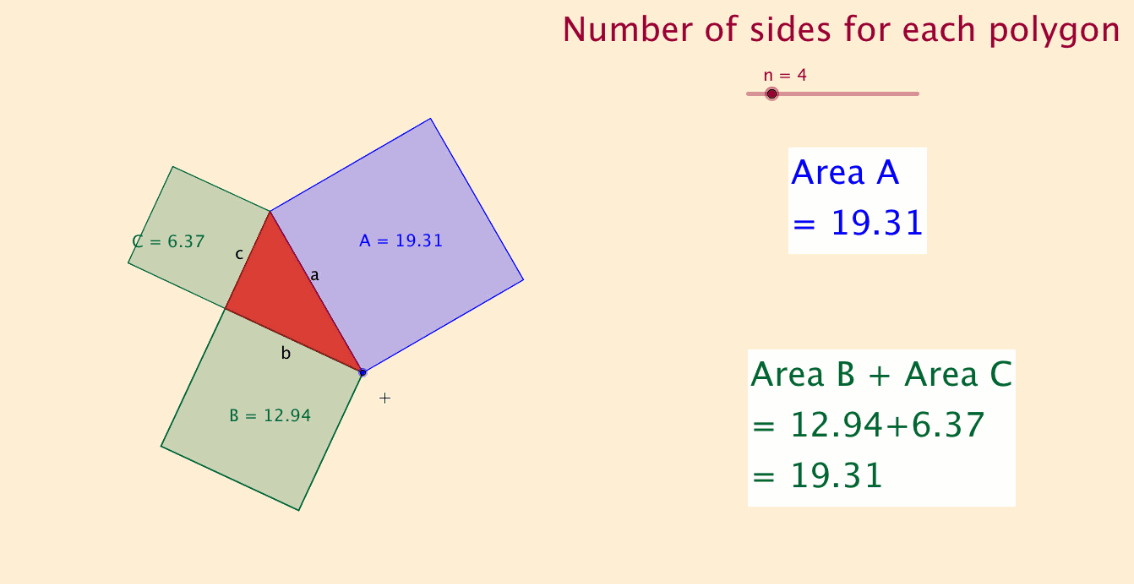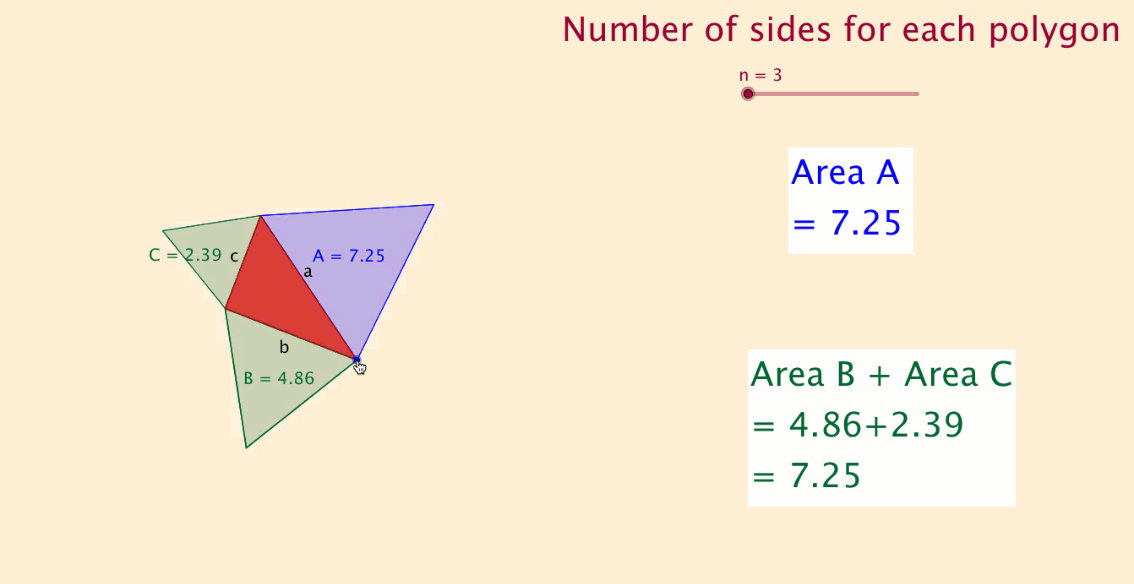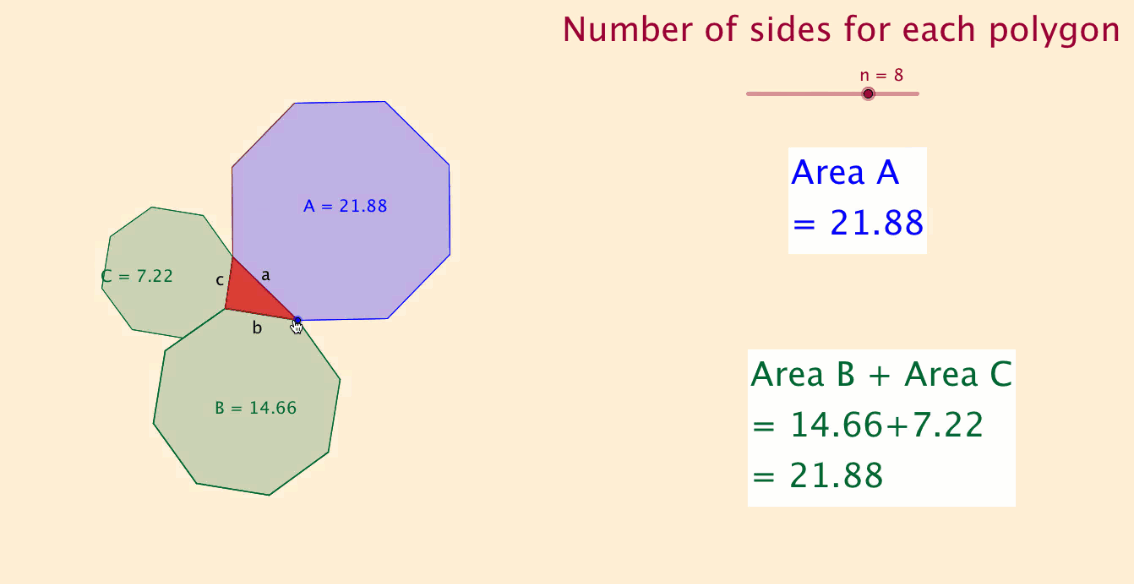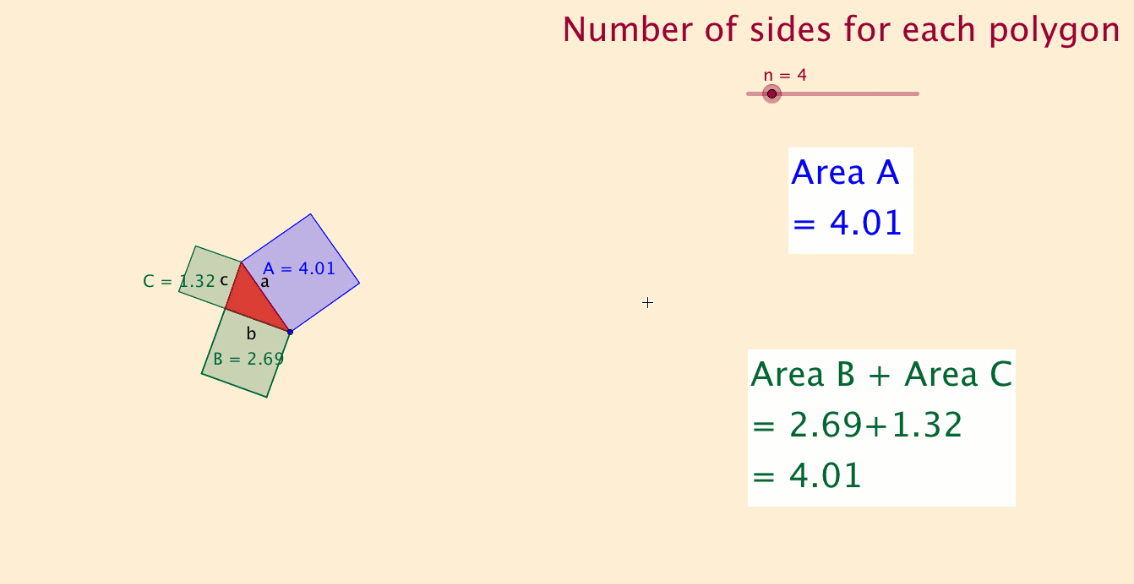
What would happen if I used equilateral triangles instead of squares on the sides of the triangle?
I investigated, and to my surprise, the theorem still held.
I then tested with other regular polygon shapes and found the same result.
I experimented with a slider with 'n' sides and found that the theorem applied to all regular polygon shapes.
The final file, shown below and at the top of this article, displays this discovery.
What would happen if I used equilateral triangles instead of squares on the sides of the triangle?
I investigated, and to my surprise, the theorem still held.
I then tested with other regular polygon shapes and found the same result.
I experimented with a slider with 'n' sides and found that the theorem applied to all regular polygon shapes.
The final file, shown below and at the top of this article, displays this discovery.
GeoGebra sparks curiosity
My Pythagoras investigation might not have uncovered anything new, but it's not the point of this article. This article highlights how GeoGebra inspired me to ask "what if" questions and led to my discovery. Without GeoGebra, I would not have pursued this investigation.
This tool caused me, a non-geeky mathematics teacher with a passion for the craft of teaching, to explore and make this discovery. The use of GeoGebra encourages curiosity and fosters a love for mathematics.
This tool caused me, a non-geeky mathematics teacher with a passion for the craft of teaching, to explore and make this discovery. The use of GeoGebra encourages curiosity and fosters a love for mathematics.
If me ... then why not students?
My point is this: If I can discover something mathematically new (to me) simply by investigating with GeoGebra then what's stopping students from gaining the same experience, especially given students have a lot more maths to discover? In the classroom students would need to be guided by a well-planned investigation - some tips are provided here - but this is all very doable. And wouldn't it be great to have our students doing some 'real' mathematics?
The important question
This leads me to an important question: Why isn’t GeoGebra (or any similar tool) an integral part of every mathematics teacher’s toolkit?
The article 'Are you utilising GeoGebra?' contains a detailed example of using a file to impart conceptual understanding (with a downloadable file). The article also argues the case for broader adoption of GeoGebra in maths classrooms across the globe
Using GeoGebra, it is surprisingly easy to improve students' conceptual understanding, as demonstrated in the article Developing conceptual understanding with GeoGebra.
Here’s what one teacher had to say after 'becoming proficient' with GeoGebra:
The article 'Are you utilising GeoGebra?' contains a detailed example of using a file to impart conceptual understanding (with a downloadable file). The article also argues the case for broader adoption of GeoGebra in maths classrooms across the globe
Using GeoGebra, it is surprisingly easy to improve students' conceptual understanding, as demonstrated in the article Developing conceptual understanding with GeoGebra.
Here’s what one teacher had to say after 'becoming proficient' with GeoGebra:
I had set out to increase my confidence with my use of GeoGebra. Richard set the course out in such a way that not only did you learn the mechanisms of GeoGebra, but it allowed you to think of other uses for the same applications. The reactions of the students at school to the (files) have∞∞ been great and it has given them more insight into some concepts that they always find difficult. Susan Hoy, 26/05/2015
Do your students make genuine mathematical discoveries? Would you like them to? Can you see how well-constructed GeoGebra investigations can help?
We'd love your thoughts below!
NOTE: Create a Hyvor account before commenting (click LOGIN) -that way you'll be notified of replies and you won't be anonymous.
If you don't create an account, please state your name at the start of your comment. Thanks.
We'd love your thoughts below!
NOTE: Create a Hyvor account before commenting (click LOGIN) -that way you'll be notified of replies and you won't be anonymous.
If you don't create an account, please state your name at the start of your comment. Thanks.